Noel recently tweeted about state machines,

and that reminded me of concurrent state machines! Those must be even cooler!

The following is an excerpt from a chapter in my upcoming book, “Essential Effects”.

Concurrent state machines

Ref and Deferred are the building blocks of concurrency within Cats Effect. With Ref we can ensure atomic updates of shared state, and Deferred gives us the ability to serialize the execution of an effect with respect to some newly-produced state. Together we can build larger and more complex concurrent behaviors. One technique to do this is to create a concurrent state machine.[1]

To build one we:

  1. Define an interface whose methods return effects.
  2. Implement the interface by building a state machine where:
    1. state (with type S) is atomically managed via a Ref[IO, S] value;
    2. each interface method is implemented by a state transition function affecting the Ref; and
    3. any state-dependent blocking behavior is controlled via Deferred values.

As an example, we’ll follow this recipe to build a structure called a countdown latch.

Example: countdown latch

The behavior we’d like to model is to block subsequent effects until a certain number of (possibly concurrent) effects have occurred.

The metaphor of a latch is used because a latch is used to keep a door closed until the latch is opened. The term countdown refers to the algorithm for how the latch is opened: a counter is decremented, and when the counter reaches zero, the latch opens.

There are two logical roles that concurrently coordinate through the shared latch:

  1. readers wait for the latch to open; and
  2. writers decrement the latch counter.

The latch itself is responsible for “opening” when its counter reaches zero.

Let’s fulfill step one of our recipe (“define an interface whose methods return effects”) by encapsulating the actions of the two roles as methods on a shared CountdownLatch interface:

trait CountdownLatch {
  def await(): IO[Unit]     // <1>
  def decrement(): IO[Unit] // <2>
}
  1. Readers will await the opening of the latch. The caller will be blocked and no value will be produced until the latch opens.
  2. Writers will decrement the latch counter, which may open the latch.

A reader will be waiting for the latch to open, perhaps denoting a set of prerequite actions have occurred:

def actionWithPrerequisites(latch: CountdownLatch) =
  for {
    _ <- IO("waiting for prerequisites").debug
    _ <- latch.await // <1>
    result <- IO("action").debug // <2>
  } yield result
  1. We block until the latch opens.
  2. Once the latch opens, we can run the action.

(In these examples, debug is an custom extension method on an IO that is essentially defined as flatTap(a => IO(println(a))), printing the value produced to the console.)

At the same time, a writer is fulfilling one or more of those prerequisites:

def runPrerequisite(latch: CountdownLatch) =
  for {
    result <- IO("prerequisite").debug
    _ <- latch.decrement // <1>
  } yield result
  1. Once the prerequisite action is completed, we decrement the latch.

Other code would run each of these roles concurrently:

val prepareAndRun =
  for {
    latch <- CountdownLatch(1)
    _ <- (actionWithPrerequisites(latch), runPrerequisite(latch)).parTupled
  } yield ()

It’s important to note that the two effects are only communicating through the shared CountdownLatch. They don’t directly know anything about each other.

When we run it we would see output like:

[ioapp-compute-1] waiting for prerequisites
[ioapp-compute-2] prerequisite
[ioapp-compute-1] action

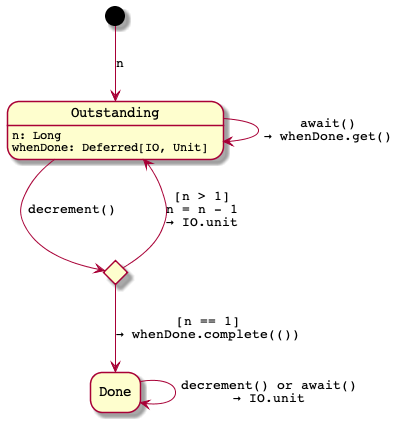
Let’s implement it! A CountdownLatch will be in one of two states:

  1. outstanding: we have n outstanding decrement() operations to expect; or
  2. done: we have invoked decrement() n (or more) times.

We’ll encode the state–step 2.1 of our recipe–as an algebraic data type:

sealed trait State
case class Outstanding(n: Long, whenDone: Deferred[IO, Unit]) extends State
case class Done() extends State

For each method of the interface, the behavior of the latch will depend on its current state:

When a reader calls await():

  • If our state is Outstanding(n, whenDone), there are n outstanding decrement calls, so block the caller via whenDone.get.
  • If our state is Done(), do nothing.

When a writer calls decrement():

  • If our state is Outstanding(n, whenDone)
    • If n is 1, this is the last decrement(). Transition to Done and unblock any blocked await() calls via whenDone.complete().
    • Otherwise decrement n.
  • If our state is Done(), do nothing.

Concurrent state machine for a countdown latch that opens after events. A holds the current state.

When we construct the CountdownLatch we’ll control concurrent access to the state with a Ref and create a Deferred to control our blocking behavior. We’ll then translate the state transitions into code almost exactly as previously described:

object CountdownLatch {
  def apply(n: Long)(implicit cs: ContextShift[IO]): IO[CountdownLatch] =
    for {
      whenDone <- Deferred[IO, Unit] // <1>
      state <- Ref[IO].of[State](Outstanding(n, whenDone)) // <2>
    } yield new CountdownLatch {
      def await(): IO[Unit] =
        state.get.flatMap { // <3>
          case Outstanding(_, whenDone) => whenDone.get // <4>
          case Done()                   => IO.unit
        }

      def decrement(): IO[Unit] =
        state.modify { // <5>
          case Outstanding(1, whenDone) => Done() -> whenDone.complete(()) // <6>
          case Outstanding(n, whenDone) =>
            Outstanding(n - 1, whenDone) -> IO.unit // <7>
          case Done() => Done() -> IO.unit
        }.flatten // <8>
    }
}
  1. We create a Deferred[IO, Unit] that we’ll use to block and unblock await() callers.
  2. We enforce atomic access to the current state with a Ref[IO, State] that we initialize to Outstanding with n expected decrements.
  3. await() never changes the state, so we only act on the value from state.get.
  4. If decrements are outstanding, we return a blocking effect that unblocks when the Deferred is completed.
  5. decrement() always changes the state, so we use Ref.modify.
  6. This is the last decrement, so we transition to Done and return an effect that completes the Deferred to unblock anyone who has invoked await().
  7. We decrement the counter and return an effect which does nothing.
  8. Our use of the state.modify method returns an IO[IO[Unit]], so we flatten it.

Voilà!

Summary

We built a countdown latch to model blocking subsequent effects until a certain number of (possibly concurrent) effects have occurred. We followed the concurrent state machine recipe:

1. Define an interface whose methods return effects.

We defined:

trait CountdownLatch {
	def await(): IO[Unit]
	def decrement(): IO[Unit]
}

2. Implement the interface by building a state machine where:

2.1. state (with type S) is atomically managed via a Ref[IO, S] value:

We initialize our state into a Ref

Ref[IO].of[State](Outstanding(n, whenDone))

where State is the algebraic data type

sealed trait State
case class Outstanding(n: Long, whenDone: Deferred[IO, Unit]) extends State
case class Done() extends State

2.2. each interface method is implemented by a state transition function affecting the Ref; and

We implement state-dependent behavior by pattern matching on the current state provided by the Ref.

Ref.modify lets us set the new state and return additional effects to be run.

2.3. any state-dependent blocking behavior is controlled via Deferred values.

We block when invoking await in the Outstanding state, and unblock any “await-ers” when invoking decrement if the counter reaches zero.

Blocking and unblocking are controlled by the get and complete methods of the whenDone: Deferred[IO, Unit] value.

By following this recipe, you too can build all sorts of control structures: mutexes, barriers, and more.

  1. Fabio Labella introduced this technique and has popularized it through his talks and public commentary. You can watch his talks and learn more at https://systemfw.org. ↩︎